DMMコース概要
複雑システムを数理モデルとして記述し、問題解決へと導く能力を養う教育プログラム。 自然科学,工学,医学などの諸問題を,現象と原理にもとづいて数理的に定式化し問題解決できる人材(数理人材)を育成
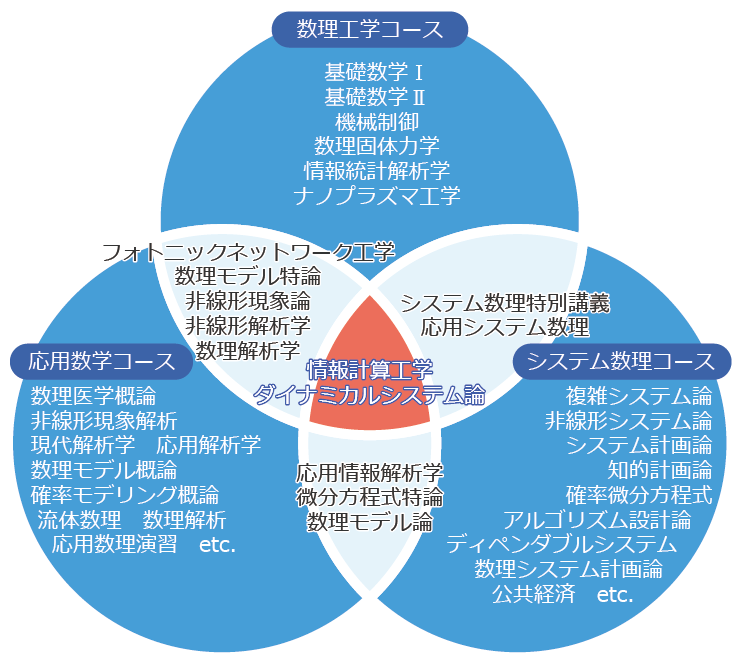
DMMでは目的に応じて3つのコースを設けます。
応用数学コース
「応用数学コース」では,現実の世界で起きるさまざまな問題を方程式などの数学的な形で表現し,論証するために必要なカリキュラムを提供します。とりわけ,自然科学,工学,医学などの諸問題を,現象と原理にもとづいて数理的に定式化し,問題解決するために必要な知識を修得します。
【応用数学コース講義例】
数理医学概論(集中講義),非線形現象解析(集中講義),数理モデル特論I, II,現代解析学I, II,応用解析学I, II,非線形数理モデルI, II, III, IV,流体数理I, II, III, IV, 確率モデリング概論,数理モデル概論,ダイナミカルシステム論,応用情報解析学,情報計算工学,応用数理演習, 数理概論I, IIなど
システム数理コース
「システム数理コース」では,数理・データ解析に基づく科学的意思決定をするために必要なカリキュラムを提供しています。製造業,流通,情報通信,金融,調査や第一次産業なども含めた様々な分野で活躍でき,数理的な技量だけでなく,対象とする現象自身を理解する能力を身に付ける教育プログラムになります。
【システム数理コース講義例】
システム数理特別講義I, II, III, IV,複雑システム論,非線形システム論,システム計画論,知的計画論,非線形数理モデル,力学系理論,微分方程式特論,確率微分方程式,情報計算工学,アルゴリズム設計論,ディペンダブルシステム,ダイナミカルシステム論,応用情報解析学,応用システム数理,数理システム計画論,公共経済I, II, 金融数理概論,金融数理特論,リスク・マネジメント など
数理工学コース
「数理工学コース」では, 工学に関する現象を数理的な問題として捉え, 現実の問題に活用出来る人材を育成します。工学,情報科学,数理科学にわたる学際的知見と現実の現象に対応する能力を身に付けることが出来ます。産業界や時代の先端を行く新しい分野で活躍でき, 技術革新と社会構造の変化に対処しうる数理的スキルを習得する教育プログラムになります。
【数理工学コース講義例】
システム数理特別講義I, II, III, IV,数理モデル特論Ⅰ,Ⅱ, 情報統計解析学, 非線形解析学, 非線形現象論, 情報計算工学, 基礎数学I,Ⅱ, 数理固体力学, 機械制御, ナノプラズマ工学, フォトニックネットワーク工学, ダイナミカルシステム論, 応用システム数理, 数理解析学など
| 目的 | 博士前期課程レベル(修士課程レベル) |
|---|---|
| 高度な数理的手法の修得 | 応用数学コース |
| 幅広い数理理論の修得と応用 | システム数理コース |
| 現象の数理的理解と応用 | 数理工学コース |