Research summary

Mathematical Modeling
and Data Science
The theory of the life science about signaling pathways in cells is constructed based on data obtained in cooperation with data science.
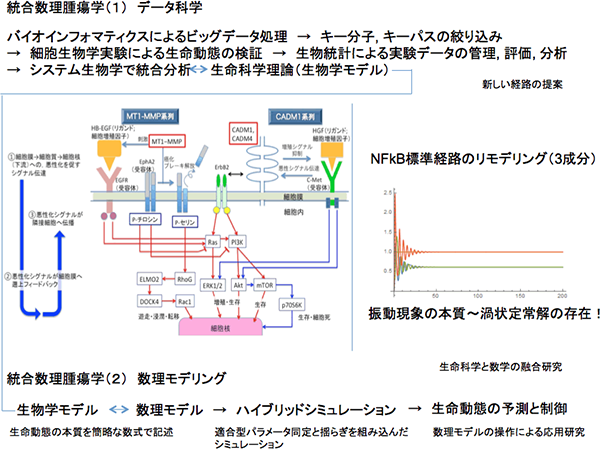
This approach is conducted in such a manner that big data is used to narrow down key paths and key molecules, cell biological experiments are conducted to verify biological dynamics, biostatistics is used to manage, evaluate, and analyze the experimental data, and systems biology is used for integral analysis.
The mathematical modeling is initiated by faithfully describing the theory of the life science with equations.
Various approaches can be used for the description.
However, a basic approach is a method for balancing movement by eliminating main factors.
In this research project, an ordinary differential equation system or a partial differential equation system is primally used, but by further adding a term contracted based on a functional relationship to the equation system, a multi-scale model is constructed in some cases.
This modeling approach aims to be not only qualitative but also quantitative.
Since the main factors are eliminated to achieve coarse graining, few basic parameters are used.
Therefore, in many cases, those parameters can be set by only adopting dimensional analysis, in addition to typical experimental values.
To verify correctness of the model, numerical simulations are adopted in the first place.
After the model is tentatively determined through the simulations, mathematical analysis is then used for remodeling to predict the life dynamics.
Also in this case, it is important to visualize a biological phenomenon through the numerical simulations.
With respect to the partial differential equations including spatial distributions in this case, the model and the numerical simulations are clearly separated from each other in consideration.
A main variable representing particles is discretely varied to give fluctuation, whereas adaptive simulations are conducted according to a trend of an environmental variable.
Such complex simulations are referred to as hybrid simulations.
A distinctive feature of the hybrid simulations is to construct particle motion and formation of its field with flexible rules by grasping the essence of the model, instead of literally and faithfully quantizing the model.
So far, I have been engaged in construction of the theory of the mathematical science and development of relevant technologies as described above, while targeting malignant progression of cancer cells, as “integral mathematical oncology”.
In this research region “mathematical signal”, this method will further be expanded to describe events penetrating a bio-hierarchy inside and outside the cell or over the cells.
This will establish a technique for unraveling the biological phenomenon.
This research project has been initiated from analysis of NFkB standard paths, and currently found out that a vibration phenomenon for signaling can be explained by using a simple dynamical system of the ordinary differential equation system, which is contracted to three components, through analysis of the classical model.
From now on, the research project will be conducted with the above mathematical analysis plan being freely used, while trying to introduce results of systems biologic methods and structural analysis.
Various approaches will be conducted such that this research region establishes a status in which the mathematical modeling assists promotion of highly-attractive wet research, and suggests new research directions.
- References
- K. Itano, T. Suzuki, Mathematical modeling and mathematical analysis of a certain pathway network of N molecules, Appl. Math. 26 (2016) 44-83
- T. Suzuki, Y. Yamada, Global-in-time behavior of Lotka-Volterra system with diffusion ? skew symmetric case, Indiana Univ. Math. J. 64 (2015) 181-216
- E.E. Espejo and T. Suzuki, Global existence and blow up for a system describing the aggregation of micoglia, Appl. Math. Lett. 35 (2014) 29-34
- A. Watanabe, D. Hoshino, N. Koshikawa, M. Seiki, T. Suzuki, K. Ichikawa, Critical role of transient activity of MT1-MMP for ECM degradation in invadopodia, PLoS Computational Biology 9-5 (2013) e1003086
- D. Hoshino, N. Koshikawa, V. Quaranta, A. Weaver, M. Seiki, K. Ichikawa, T. Suzuki, Establishment and validation of computational model for MT1-MMP dependent ECM degradation and intervention strategies, PLoS Computational Biology 8-4 (2012) 21002479
- K. Nakane, M. Gameiro, N. Matsuura, T. Suzuki, Development of a cancerous lesion tissue extraction method with an algorithm based on a topologic approach, Appl. Math. 22 (2012) 97-108
- T. Saitou, M. Rouzimaimaiti, N. Koshikawa, M. Seiki, K. Ichikawa, T. Suzuki, Mathematical modeling of invadopodia formation, J. Theoretical Biology 298 (2012) 138-146
- E.E. Espejo, A. Stevens, T. Suzuki, Simultaneous blowup and mass separation during collapse in an interacting system of chemotactic species, Differential Integral Equations 25 (2012) 251-288
- T. Suzuki, Cellular molecules and mathematics relating to tumorigenesis ? top-down modelling and key path search, Appl. Math. 21 (2011) 50-54
- K. Ichikawa, T. Suzuki, N. Murata, Stochastic simulation of biological reactions, and its applications for studying actin polymerization, Physical Biology 7 (2010) 046010
PAGE TOP

